Vortriebsverhältnis: Unterschied zwischen den Versionen

Aus WikiPedalia
Zeile 37: Zeile 37:
===Wie verhält es sich mit Kurbellängen?===
===Wie verhält es sich mit Kurbellängen?===


:Alle diese Systeme haben eine gemeinsame Ungenauigkeit: Keines bezieht die Kurbellänge mit ein. Faktisch ist die Mountainbike-Übersetzung 46/16 nur dann mit der Rennrad-Übersetzung 53/19 vergleichbar, wenn beide die gleiche Kurbellänge benutzen. Falls das Mountainbike jedoch eine 175mm-Kurbel und das Rennrad eine 170mm-Kurbel verbaut hat, reduziert sich die Übersetzung am Mountainbike tatsächlich um rund drei Prozent.
:Alle diese Systeme haben eine gemeinsame Unschönheit: Keines bezieht die Tretkurbellänge (Länge des Pedalarms) mit ein! Gefühlt ist die Mountainbike-Übersetzung 46/16 aber nur dann mit der Rennrad-Übersetzung 53/19 gleich, wenn beide die gleiche Tretkurbellänge benutzen. Falls das Mountainbike jedoch eine 175mm-Kurbel und das Rennrad eine 170mm-Kurbel verbaut hat, reduziert sich die Übersetzung (von Fußbewegungsweg auf Fahrstrecke) am Mountainbike tatsächlich um rund drei Prozent.


==Vorschlag für einen neuen Standard==
==Vorschlag für einen neuen Standard==

Version vom 27. Juli 2017, 11:05 Uhr

Gain Ratio - Die Sheldon Brown-Methode zur Berechnung des Vortriebsverhältnisses

Bestimmung von Fahrrad-Übersetzungen

Fahrradfahrer finden es häufig nützlich, eine numerische Angabe zu den Übersetzungen ihrer Fahrräder zur Hand zu haben. Diese Angaben erlauben es ihnen, aussagekräftige Kriterien zur persönlichen Anpassung ihrer Übersetzungen auszudrücken und machen außerdem die Leistungsfähigkeit einzelner Fahrräder untereinander vergleichbar.

Hierzu gibt es mehrere Systeme, keines scheint vollständig zufrieden stellend zu sein. An dieser Stelle soll ein Vorschlag für ein neues, akkurateres und universelleres System vorgestellt werden.

Existierende Systeme

Vorne/Hinten

Fahrradfahrern, die nur mit einem sehr eng begrenzten Umfeld der Fahrradwelt in Berührung kommen, reicht oft die Kettenblatt- und Ritzelgröße, die sie in Benutzung haben. Jedoch erscheint es lästig und verwirrend, zwei Zahlen benutzen zu müssen, obwohl man doch nur eine Zahl bräuchte. 39/14 entspricht zum Beispiel 53/19, auch wenn es nicht auf den ersten Blick erkennbar ist. Da bei Rennrädern für gewöhnlich vorne nur vier Kettenblattgrößen in Gebrauch sind (39, 42, 52 und 53), ist dies noch überschaubar für Fahrradfahrer, die nur mit dieser Art Räder in Berührung kommen.
Radler, die vermutlich mit einem weiteren Spektrum an Kettenblättern vorn, Ritzeln hinten und Reifengrößen (hinten) zu schaffen haben, benötigen ein weiterentwickeltes System, um zu ersehen, dass 46/16 am Mountainbike, 42/12 am "Moulton" und 52/14 an Ihrem "Bike Friday" das gleiche wie die schon erwähnten 39/14 und 53/19 am Rennrad sind.
Dieses System ist aber nicht mehr anwendbar, sobald ein Planetengetriebe ins Spiel kommt.

Zölliger Übersetzungsdurchmesser (Gear Inch)

Das einfachste gebräuchliche System in USA - nicht aber in Europa - ist das "Gear Inch"-System. Es datiert auf die Zeit vor dem Kettenantrieb bei Fahrrädern zurück. Es bezeichnete ursprünglich den Durchmesser des Vorderrads bei Hochrädern. Als kettengetriebene "Sicherheitsräder" aufkamen, wurde das gleiche System weiterverwendet, wobei der Durchmesser des Antriebsrades mit dem Zahnverhältnis multipliziert wurde. Es ist sehr einfach zu berechnen:

Vortriebsverhältnis GearInch Formel.png

Mit:

  • I = Übersetzungsdurchmesser in Zoll
  • T = Zahl der Zähne (f=Front, r=Rear)
  • d = Durchmesser in Zoll

Dies ergibt einen einzelnen zwei- bis dreistellige Zahlenwert. Die oben erwähnten Beispiele liegen bei rund 74-75 Zoll. Die kleinste Übersetzung bei Mountainbikes beträgt in der Regel rund 22-26 Zoll. Die höchsten Übersetzungen haben Rennräder mit rund 108-110 Zoll. Jedoch ist absehbar, dass für zollbasierte (nicht-metrische, nicht SI) Messgrößen die Zeit abgelaufen ist (dachte man vor 2000).

Entfaltung in Metern

In Ländern mit metrischen Messsystemen wird überwiegend mit Entfaltung in Metern gerechnet. Das ist die Distanz, die ein Fahrrad mit jeder Kurbelumdrehung vorwärts bewegt wird. Dieses System ist aus zwei Gründen für Nicht-Metrische etwas lästiger als das "Gear Inch" System:
  1. Es ist etwas schwieriger, 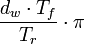Entfaltung in Metern.png (dw=Reifendurchmesser in Metern, Tf = Zähnezahl vorderes Ritzel, Tr = Zähnezahl hinteres Ritzel) zu rechnen, denn die Multiplikation mit einer irrationalen Zahl Pi verkompliziert die Rechnung.
  2. Das Ergebnis ist eine Zahl mit zwei Dezimalstellen und somit weniger leicht zu handhaben.
    • Beispiel: 52/13 (Zähne) mal 28" ergibt Rennrad IG = 112 Zoll und entspräche 8,64 Meter pro Kurbeldrehung. 24T/28T am Mountainbike käme 1,78 Meter / Drehung gleich.

Wie verhält es sich mit Kurbellängen?

Alle diese Systeme haben eine gemeinsame Unschönheit: Keines bezieht die Tretkurbellänge (Länge des Pedalarms) mit ein! Gefühlt ist die Mountainbike-Übersetzung 46/16 aber nur dann mit der Rennrad-Übersetzung 53/19 gleich, wenn beide die gleiche Tretkurbellänge benutzen. Falls das Mountainbike jedoch eine 175mm-Kurbel und das Rennrad eine 170mm-Kurbel verbaut hat, reduziert sich die Übersetzung (von Fußbewegungsweg auf Fahrstrecke) am Mountainbike tatsächlich um rund drei Prozent.

Vorschlag für einen neuen Standard

An dieser Stelle soll ein neues System vorgestellt werden, welches Kurbellängen mit einbezieht. Das System ist unabhängig von Messeinheiten und wird in einem reinen Verhältnis ausgedrückt.

Dieses Verhältnis wird wie folgt berechnet: Vortreibsverhältnis die Formel.png

  1. Der Laufradradius wird durch die Kurbellänge geteilt. Das Resultat ist ein einzelnes Radienverhältnis, das für alle Übersetzungen des Fahrrads angewendet werden kann.
  2. Die individuellen Übersetzungsverhältnisse werden wie beim "Gear Inch" System berechnet. Nur verwendet man anstelle der Laufradgröße das Radienverhältnis. Diese Zahl ist ein reines Verhältnis, Einheiten werden herausgekürzt.
Das Ergebnis ist das "Vortriebsverhältnis" (oder "Gain Ratio" auf englisch).

Einzelne Gänge werden wie folgt berechnet:
Radienverhältnis x Zähnezahl vorderes Kettenblatt / Zähnezahl hinteres Ritzel

Beispiele 

Ein Rennrad hat eine Kurbellänge von 170mm und einen Laufradradius von 340mm (Rennradlaufräder haben einen generischen Durchmesser von 680mm).

340mm/170mm = 2 (Radienverhältnis)

Vortriebsverhältnis: 2,0 x 53 / 19 = 5,58

Das heißt, dass für jeden Zoll, Kilometer oder jede preußische Meile, das ein Pedal auf seiner Umlaufbahn um das Innenlager zurücklegt, das Fahrrad 5,58 Zoll, Kilometer oder preußische Meilen zurücklegt, wenn vorne das Kettenblatt mit 53 und hinten das Ritzel mit 19 Zähnen aufgelegt wird.

Ein Mountainbike mit 26 Zoll-Laufrädern (330 mm Radius) und 175 mm Kurbeln:

330mm/175mm = 1,89

Vortriebsverhältnis: 1,89 x 32 / 16 = 3,78 (Für Kettenblatt = 32 Zähne und Ritzel = 16 Zähne)

Zur Erinnerung: Das Radienverhältnis muss nur einmal pro Fahrrad berechnet werden, da es für alle Übersetzungen gleich ist.
Es darf jede Maßeinheit benutzt werden, solange diese jeweils für Reifengröße und Kurbellänge gleich ist.

Vortriebsverhältnisse für gebräuchliche Kurbellängen

Reifengröße Reifenradius
in mm		 165 mm 170 mm 172.5 mm 175 mm 180 mm
I.S.O. 630:
27 X 1 3/8 345 2.091 2.029 2.000 1.971 1.917
27 X 1 1/4 343 2.079 2.018 1.988 1.960 1.906
27 X 1 1/8 342 2.073 2.012 1.983 1.954 1.900
27 X 1 340 2.061 2.000 1.971 1.943 1.889
I.S.O. 622:
700 X 56 370 2.242 2.176 2.145 2.114 2.056
700 X 50 365 2.212 2.147 2.116 2.086 2.023
700 X 44 354 2.145 2.082 2.052 2.023 1.967
700 X 38 347 2.103 2.041 2.012 1.983 1.927
700 X 35 345 2.091 2.029 2.00 1.971 1.917
700 X 32 342 2.073 2.012 1.983 1.954 1.900
700 X 28 336 2.036 1.976 1.948 1.920 1.867
700 X 25 335 2.030 1.971 1.942 1.914 1.861
700 X 20 332 2.012 1.953 1.925 1.897 1.844
I.S.O. 559:
26 X 2.125 330 2.000 1.941 1.913 1.886 1.833
26 X 1.9 324 1.964 1.906 1.878 1.851 1.800
26 X 1.5 312 1.891 1.835 1.809 1.783 1.733
26 X 1.25 311 1.884 1.829 1.803 1.778 1.728
26 X 1.0 (559 mm) 305 1.848 1.794 1.768 1.743 1.694
I.S.O. 571:
26 x 1 (650C) 311 1.884 1.829 1.803 1.778 1.728
Andere
Breiter
Schlauchreifen		 338 2.048 1.988 1.959 1.931 1.878
Schmaler
Schlauchreifen		 335 2.030 1.971 1.942 1.914 1.861
26 X 1 3/8 (590 mm) 330 2.000 1.941 1.913 1.886 1.933
24" 305 1.848 1.794 1.768 1.743 1.694
24 x 1 (520 mm) 279 1.691 1.641 1.617 1.594 1.550
20 X 1.75 (406 mm) 254 1.539 1.494 1.472 1.451 1.411
20 X 1 1/4 (451 mm) 257 1.558 1.512 1.490 1.469 1.428
17 x 1 1/4 (369 mm) 211 1.279 1.241 1.223 1.206 1.172
16 x 1 3/8 (349 mm) 204 1.236 1.200 1.183 1.166 1.133

Externe Links

Sheldon Browns Online Gear Calculator

Werbung:

Quellen

Abgerufen von „https://wikipedalia.com/index.php?title=Vortriebsverhältnis&oldid=13277“